Transformer on load Condition
Transformer on load Condition: When load is connected to the secondary winding of a transformer , I2 (secondary current) is set up in the secondary winding. The magnitude and phase of I2 with respect to V2 (secondary voltage) depends upon the characteristics of the load. Secondary current I2 is in phase with V2,if load is no inductive , lags if load is inductive and it leads if load is capacitive.
This secondary current sets up m.m.f( =N2I2 ) and hence it produce magnetic flux Φ 2 which is in opposition to the main primary flux Φ . The secondary ampere-turns N2I2 are known as demagnetizing amp-turns. The opposing secondary flux Φ 2 weakens the primary flux Φ momentarily, hence the primary winding back e.m.f E1 tends to be reduced. For a moment V1 > E1 and hence more current to flow in the primary winding . Let the additional primary current be I2’ which is known as load component of primary current. This current (I2) is anti-phase with I2.This load component of primary current(I2’) sets up its own flux Φ 2’ which is in opposition to secondary flux Φ 2 , but is in the same direction as primary flux Φ. And flux Φ 2’ is equal to Φ 2. Hence, the two flux cancel each other out.
So, we can say that whatever the load conditions, the net flux passing through the core is approximately the same as at no-load. Due to the constancy of core flux at all loads, the core loss is also practically the same under all load conditions.
As Φ 2= Φ 2’
Hence, when transformer is no load, the primary winding has two currents in it; one is I0 and the other is I2’ which is anti-phase with I2 and K times in magnitude. The total primary current is the vector sum of I0 and I2’.
In Fig. shown the vector diagram of a transformer when the load is non-inductive and when the load is inductive.
If we assume voltage transformation ratio is unity , ( i.e K= 1 )
In the fig.-1, shown the vector diagram of a transformer when load is non-inductive
I2= secondary current in phase with E2= V2
I2’= load component of primary current which is anti-phase with I2 and also equal to it in magnitude( as K=1 )
I1= Primary current which is vector sum of I0 and I2’ and lags behind V1 by angle φ1.
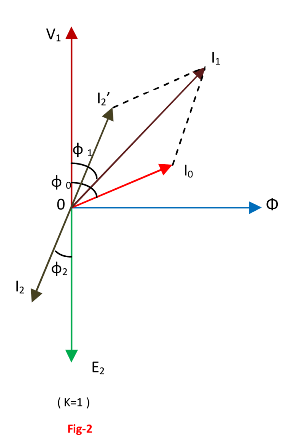
In the fig.-2, shown the vector diagram of a transformer when load is inductive,
I2= secondary current lags E2 by φ2.
I2’= load component of primary current which is anti-phase with I2 and also equal to it in magnitude( as K=1 )
I1= Primary current which is vector sum of I0 and I2’ and lags behind V1 by angle φ1.
It is seen from the fig.-2 that the angle φ1is slightly greater than φ2.
In figure , It is seen that I0 is neglect as compared to I2’, then φ1= φ2.
Besides, under this assumption ,
N1I2’= N2I1= N1I2
It is shown that under the full-load condition, the ratio of primary and secondary current is constant. The relationship is made the basis of current transformer, such a transformer which is used with a low-range ammeter for measuring currents in circuits.
