

In these topics, it is discussed the voltage distribution over suspension insulator string. Let, there are 5 nos. disc insulators which are connected in series through metallic link and suspense from line tower which is shown in the figure. From the figure, it is seen that porcelain portion of each disc is in between two metal links.

Therefore each disc forms a capacitor C as shown in fig. It is known as mutual capacitance or self-capacitance. And capacitance also exists between metal fitting of each disc and tower or earth. This is known as shunt capacitance mc. Due to the shunt capacitance, the charging current is not the same though all the disc of string. Hence, the voltage across each disc will be different. And voltage across to the nearest conductor will have the maximum voltage. The reference to Fig. V5 will be much than V4 or V3 or V2 or V1.
The following points may be noted regarding the potential distribution over a string of suspension insulators:
The Ratio of the voltage across the whole string to the product of numbers of discs and the voltage across the disc nearest to the conductor is known as string efficiency.
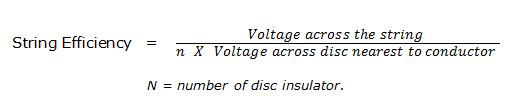
String efficiency is important for the overhead transmission line. The greater the string efficiency, the more uniform is the voltage distribution in the each disc insulator. In the ideal case, the value of string efficiency will be 100%, but, in a normal case, it is impossible to achieve 100% string efficiency, yet effort should be made to improve it as close to this value as possible.
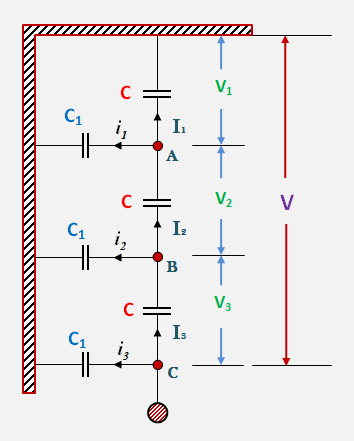
Fig. shows the equivalent circuit for a 3-disc string. Let us suppose that self-capacitance of each disc is C1 , Let us further assume that shut capacitance C1 is some fraction K of self –capacitance i.e., C1 =KC. Starting from the cross –arm or tower , the voltage across unit is V1 , V2 , V3 respectively as shown.
Applying Kirchhoff’s current law to node A, we get , I2 =I1 + i1 Or, V2ωC = V1ωC + V1ωC1 Or, V2ωC = V1ωC + V1ωKC V2=V1(1+K).................(i)
Applying Kirchhoff’s current law to node B, we get , I3 = I2 + i2 Or V3ωC = V2ωC +(V1+V2) ωC1 Or V3ωC = V2ωC +(V1+V2) ωKC Or V3=V2+(V1+V2) K =KV1+V2(1+K) =KV1+V1(1+K)2 =V1[K+(1+K)2] V3=V1[1+3K+K2].................(ii)
Voltage between conductor and earth ( i,e., tower) V = V1 + V2 + V3 =V1+V1(1+K)+V1(1+3K+K2) =V1(3+4K+K2)
Voltage across second unit from top , V2 = V1 (1 +K)
Voltage across third unit from top, V3= V1( 1 +3K + K2) The following points may be noted from the above mathematical analysis: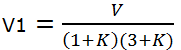 .................(iii)
.................(iii)
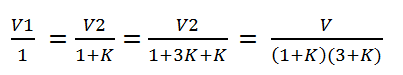

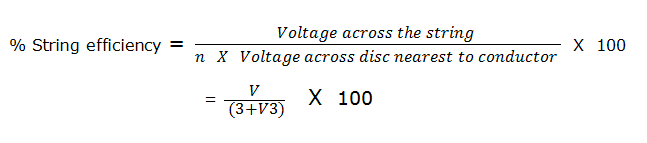
More details